
|
One-liner pictures -- Grow a picture from a line of C code |
|
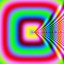
Here is the picture corresponding to the C-language expression in the form above:
Is this picture not what you expected? Check here. (The picture is an uncompressed .bmp so it is easy to download and save as a test image. The original purpose of one-liner pictures was fast and easy test image creation.) |
Copy/paste these into the form then edit to produce variants.
|
Three ways to make an impulse (x == 0 && y == 0) ? 1 : 0 x || y ? 0 : 1 !(x || y) Notice that all generated pictures are re-ranged to [0,255]. |
 |
|
Green diamond abs(x)+abs(y) < 80 ? green : 0 |
 |
|
Circular cosine cos(sqrt(x*x+y*y)/10.0) Because of re-ranging, this is just as good as: 128 + 127*cos(sqrt(x*x+y*y)/10.0) |
 |
|
A coloured field abs(x-y)*red + (127-x)*green + (y+128)*blue |
 |
|
A [-green,green] ramp y*green Why does a green ramp have other colours? Because the range of values of y is [-128,127], so when the picture is re-ranged, 128 gets added to all of red, green and blue. If you want a pure green ramp, you have to do: (y+128)*green |
 |
|
Uniformly distributed noise rand() % 256 (The random number generator used here is believed to be random in its lower-order bits.) |
 |
|
Swiss flag. abs(x) < 25 && abs(y) < 75 || abs(x) < 75 && abs(y) < 25 ? white : 0.8*red For a colour image, you can multiply by white as shorthand for multiplying red, green and blue equally. |
 |
|
Gaussian hill exp(-0.5*(x*x/8000.0+y*y/3000.0)) Just the central part of an axis-oriented 2D gaussian function. Note the use of real constants (with decimal point) to ensure floating-point arithmetic. |
 |
|
Bulb abs(x*x*x + y*y*y) < 90*90*90 ? 128*green + (128+x)*red + (255-abs(x+y))*blue : 0 |
 |
|
Checkerboard x & 32 ^ y & 32 ? 0 : 1 Try "x & 32 ^ y & 32 ? x : y" for a strange variation. |
 |
|
Colour bars green * (x < 0) + red * (x < 0 ? x < -64 : x < 64) + blue * (x < 0 ? x < -64 ? x < -96 : x < -32 : x < 64 ? x < 32 : x < 96) Not the easiest way to generate colour bars but demonstrates multiplication by a condition. |
 |
|
Painterly colour bars sin(x/40.0)*green + cos(x/40.0)*red + sin(-x/40.0)*blue |
 |
|
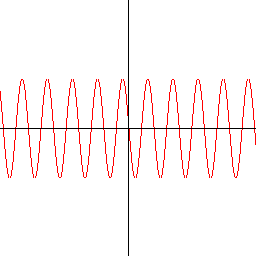
A sine wave graph x == 0 ? 0 : y == 0 ? 0 : (y-50*sin(x/4.0))*(y-50*sin((x-1)/4.0))<0 ? red : white To draw graphs like this, you have to detect zero-crossings. |
 |
|
Gabor filter point spread function exp(-0.5*(x*x/(20.0*20)+y*y/(20.0*20)))*cos(x/4.0) |
 |
|
Another Gabor filter (different variance, centre frequency and orientation) exp(-0.5*(x*x/(30.0*30)+y*y/(30.0*30)))*cos((x*cos(1)+y*sin(1))/3.0) |
 |
|
Smiley x*x + y*y > 82*82 ? white : x*x + y*y >= 80*80 || (x+30)*(x+30)+(y+20)*(y+20) < 12*12 || (x-30)*(x-30)+(y+20)*(y+20) < 12*12 || x*x + (y+30)*(y+30) >= 80*80 && x*x+(y+30)*(y+30)<=82*82 && y > 30 ? 0 : red + green |
 |
|
Face x<0||y<0||x>15||y>15?0:x&8?y&8?x&4?y&4?x&2?y&2?x&1?y&1?87:104:y&1? 109:90:x&1?y&1?126:142:y&1?98:114:y&2?x&1?y&1?102:90:y&1?116: 126:x&1?y&1?111:139:y&1?143:148:x&2?y&2?x&1?y&1?153:153:y&1?117: 132:x&1?y&1?160:169:y&1?142:158:y&2?x&1?y&1?168:141:y&1?154:120: x&1?y&1?160:179:y&1?128:178:y&4?x&2?y&2?x&1?y&1?175:150:y&1?184: 135:x&1?y&1?126:137:y&1?124:146:y&2?x&1?y&1?187:137:y&1?192:135: x&1?y&1?134:152:y&1?169:143:x&2?y&2?x&1?y&1?100:84:y&1?66:117:x&1? y&1?105:114:y&1?116:116:y&2?x&1?y&1?117:123:y&1?150:152:x&1?y&1? 108:95:y&1?96:94:x&4?y&4?x&2?y&2?x&1?y&1?179:190:y&1?176:186:x&1? y&1?194:189:y&1?197:157:y&2?x&1?y&1?195:202:y&1?205:208:x&1?y&1? 192:136:y&1?157:152:x&2?y&2?x&1?y&1?167:159:y&1?113:116:x&1?y&1? 158:185:y&1?93:141:y&2?x&1?y&1?112:120:y&1?127:112:x&1?y&1?134: 102:y&1?128:101:y&4?x&2?y&2?x&1?y&1?189:201:y&1?106:190:x&1?y&1? 162:173:y&1?195:161:y&2?x&1?y&1?145:138:y&1?153:134:x&1?y&1?167: 153:y&1?137:99:x&2?y&2?x&1?y&1?110:120:y&1?192:120:x&1?y&1?106: 115:y&1?78:129:y&2?x&1?y&1?112:105:y&1?94:123:x&1?y&1?132:135:y&1? 178:121:y&8?x&4?y&4?x&2?y&2?x&1?y&1?199:147:y&1?196:165:x&1?y&1? 169:160:y&1?151:138:y&2?x&1?y&1?143:160:y&1?87:112:x&1?y&1?166: 173:y&1?134:134:x&2?y&2?x&1?y&1?152:170:y&1?120:172:x&1?y&1?95: 162:y&1?134:194:y&2?x&1?y&1?130:164:y&1?127:139:x&1?y&1?161:170:y&1? 137:148:y&4?x&2?y&2?x&1?y&1?143:114:y&1?139:116:x&1?y&1?122:142: y&1?118:125:y&2?x&1?y&1?140:120:y&1?168:148:x&1?y&1?124:128:y&1? 156:154:x&2?y&2?x&1?y&1?142:116:y&1?142:159:x&1?y&1?142:189:y&1? 170:187:y&2?x&1?y&1?113:90:y&1?147:124:x&1?y&1?111:128:y&1?111: 129:x&4?y&4?x&2?y&2?x&1?y&1?201:183:y&1?229:214:x&1?y&1?155:168: y&1?197:194:y&2?x&1?y&1?188:188:y&1?189:207:x&1?y&1?190:149:y&1? 163:148:x&2?y&2?x&1?y&1?186:184:y&1?191:188:x&1?y&1?95:120:y&1? 140:86:y&2?x&1?y&1?111:133:y&1?66:89:x&1?y&1?118:129:y&1?169:119: y&4?x&2?y&2?x&1?y&1?202:195:y&1?198:204:x&1?y&1?165:178:y&1?174: 147:y&2?x&1?y&1?158:178:y&1?135:110:x&1?y&1?188:178:y&1?87:78: x&2?y&2?x&1?y&1?128:88:y&1?89:102:x&1?y&1?146:101:y&1?155:85:y&2? x&1?y&1?167:85:y&1?82:85:x&1?y&1?163:202:y&1?71:112 Obviously this one is generated by a program. It could be shorter -- note the substring "y&1?:188:188" -- but let's face it, this is not the way to make photographs! |
 |